サイクロイドのいろいろな特徴（１）
(2016年10月15日)
早くゴールに着くのはどのコース？
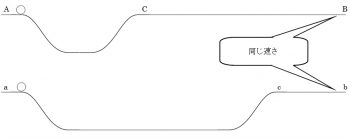
下の図のように、深さが同じで長さが違う谷がある、２つのコースがあります。
この２つのコース上のスタート地点 Aとa にある物体が、同時に同じ速さで滑り始めるとします。さて、どちらの方が先にゴール（Bあるいはb）に着くでしょうか。
そうそう。この手の問題のお約束として、摩擦抵抗・空気抵抗は無視できるものとします。
高校物理で学習する「力学的エネルギー保存の法則」により、谷を登り切ったときの（Cあるいはc での）速さは同じはずですから、ゴールであるBとbそれぞれに到着するときの速さは同じはずです。
だとすると、ゴールにも同時に到着するでしょうか。
いえ。 速く動いている谷底での道のりが長い、下のコースを進む方が早くゴールに着きます。
https://www.youtube.com/watch?v=cUgDE_Lh294
上のコースでは、スタート地点のAあるいはaから物体が滑り落ちるときの坂の部分はおなじものでした。では、２地点間を物体が滑り落ちるとき、道筋が異なると移動に要する時間はどうなるでしょうか。
具体的に考えてみましょう。
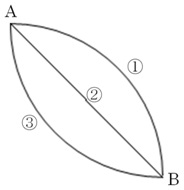
左図の地点Aから滑り落ちる物体が一番早く地点Bに到達するのは、①, ②, ③ のどのコースでしょうか。
上の例から考えると、速く動く時間が長いほうが早くゴールにたどりつくと考えられます。
コース① はなかなか速くならないですが、コース③ はすぐに速くなります。したがって、コース③ が一番早くゴールに着くということが予想されます。
ところで、このコース①, ③は、どちらも円の一部（円弧）ですが、似たような曲線は、双曲線、放物線、楕円など他にもたくさんあります。
では、一番早くゴールに着くのはどのような曲線なのでしょうか。つまり、一番早く「速くなる」曲線は、どのような曲線なのでしょうか。
サイクロイド曲線
コース ③のような曲線のうち、もっとも早くゴールに着く曲線は、サイクロイド曲線と呼ばれる曲線です。
サイクロイド曲線とは、直線に沿って円が回転するときの円周上の点の軌跡のことです。
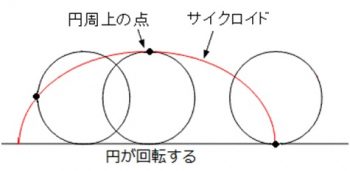
このサイクロイド曲線、物理的にも数学的にもなかなか面白い性質を持っています。
数学的な面では、たとえば、上の図で円の半径をaとすると、円１回転分の曲線の長さは8a、曲線で囲まれる部分の面積は3πa2という値となります。
物理的な面では、最速降下曲線と呼ばれること、サイクロイド振り子という振幅が変わっても周期が変わらない振り子の軌道、サイクロイド軌道での物体の落下時間の等時性、があります。
１．最速降下曲線
先程のコース③のような曲線のうち、サイクロイド曲線（上の図の赤線の曲線を上下反転させた曲線）は、2点間を物体が最も速く滑り落ちる曲線です。サイクロイド曲線の作り方からすぐに想像できると思いますが、上下反転させたサイクロイド曲線は、出発点は垂直になっているのですぐに速くなります。これも、最も速く滑り落ちる曲線と呼ばれる由縁の一つです。
新潟工科大学の竹野氏が詳しく解説をしておられます。
http://takeno.iee.niit.ac.jp/~shige/math/lecture/misc/data/cycloid1.pdf
(続く）
村石 幸正（むらいし ゆきまさ）
教育に関する遺伝と環境からの影響を調べるため、募集枠を設けて双生児を入学させている東京大学教育学部附属中等教育学校で、長年にわたり、理科・物理の教員を務め、放射線教育に関わると共に、双生児研究に携わってきた。
現在、中央大学理工学部に教職課程担当の特任教授として勤務。